This section explains the data type and the internal data representation. The internal data representation is determined according to the following four items:
Shows the memory size necessary to store the data.
Restricts the addresses to which data is allocated. There are three types of alignment; 1-byte alignment in which data can be allocated to any address, 2-byte alignment in which data is allocated to even byte addresses, and 4-byte alignment in which data is allocated to addresses of multiples of four bytes.
Shows the range of data of scalar type (C) or basic type (C++).
Shows an example of assignment of element data of compound type (C) or class type (C++).
Table 4.1 shows internal representation of scalar type data in C and basic type data in C++.
When the signed_char option is specified, the char type has the same value range as the signed char type. |
When the int_to_short option is specified, the int type has the same value range as the short type, the signed int type has the same value ranges as the signed short type, and the unsigned int type has the same value range as the unsigned short type. |
When the auto_enum option is specified, the smallest type that holds enumeration values is selected. |
This data type is only valid for compilation of C++ programs or C programs including stdbool.h. |
Pointers to function and virtual function members are represented in the following data structure. |
This data type is only valid when compiling a C99 program or C program in which stdbool.h has been included. |
When C89 is used for compiling, the size, number of bytes for alignment, and sign are the same as for the unsigned long type. |
This section explains internal representation of array type, structure type, and union type data in C and class type data in C++.
Table 4.2 shows internal representation of compound type and class type data.
In the following examples, a rectangle ( ) indicates four bytes. The diagonal line (
) indicates four bytes. The diagonal line (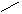 ) represents an unused area for alignment. The address increments from right to left (the left side is located at a higher address).
) represents an unused area for alignment. The address increments from right to left (the left side is located at a higher address).
When structure members are allocated, an unused area may be generated between structure members to align them to boundaries.

If a structure has 4-byte alignment and the last member ends at an 1-, 2-, or 3-byte address, the following three, two, or one byte is included in this structure.

When an union has 4-byte alignment and its maximum member size is not a multiple of four, the remaining bytes up to a multiple of four is included in this union.
For classes having no base class or virtual functions, data members are allocated according to the allocation rules of structure data.

If a class is derived from a base class of 1-byte alignment and the start member of the derived class is 1-byte data, data members are allocated without unused areas.

For a class having a virtual base class, a pointer to the virtual base class is allocated.

For a class having virtual functions, the compiler creates a virtual function table and allocates a pointer to the virtual function table.

An example is shown for class having virtual base class, base class, and virtual functions.

For an empty class, a 1-byte dummy area is assigned.

For an empty class having an empty class as its base class, the dummy area is one byte.

Dummy areas shown in the above two examples are allocated only when the class size is 0. No dummy area is allocated if a base class or a derived class has a data member or has a virtual function.

A bit field is a member allocated with a specified size in a structure, a union, or a class. This section explains how bit fields are allocated.
Table 4.3 shows the specifications of bit field members.
The bool type is only valid for compilation of C++ programs or C programs including stdbool.h. |
To use a bit field member, data in the bit field is extended to the declared type. One-bit field data declared with a sign is interpreted as the sign, and can only indicate 0 and −1. |
Sign extension: The most significant bit of a bit field is used as a sign and the sign is written to the upper bits to extend data. |
This data type is only valid for programs in C99. The _Bool type is treated as the bool type in compilation. |
Bit field members are allocated according to the following five rules:
Bit field members are placed in an area beginning from the right, that is, the least significant bit. |

Consecutive bit field members having type specifiers of the same size are placed in the same area as much as possible. |

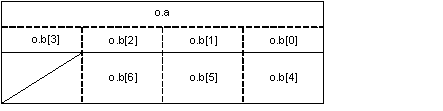
If the number of remaining bits in an area is less than the next bit field size, even though the type specifiers indicate the same size, the remaining area is not used and the next bit field is allocated to the next area. |
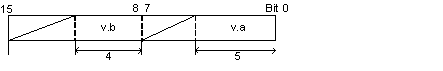
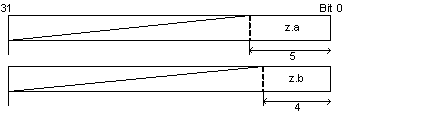
If a bit field member with a bit field size of 0 is declared, the next member is allocated to the next area. |

It is also possible to place bit field members from the upper bit. For details, refer to the description on the bit_order option in Compiler Options, and the description on #pragma bit_order in 4.2 Extended Language Specifications. |
In big endian, data are allocated in the memory as follows:
The order of bits in one-byte data for the little endian and the big endian is the same.
The upper byte and the lower byte will be reversed in two-byte data between the little endian and the big endian.
Little Endian: Address 0x100: 0x34 Big Endian: Address 0x100: 0x12
Address 0x101: 0x12 Address 0x101: 0x34
The order of bytes will be reversed in four-byte data between the little endian and the big endian.
When the int_to_short option is specified, the signed int and unsigned int types have the same size and number of bytes for alignment as the signed short and unsigned short types, respectively. |
Little Endian: Address 0x100: 0x78 Big Endian: Address 0x100: 0x12
Address 0x101: 0x56 Address 0x101: 0x34
Address 0x102: 0x34 Address 0x102: 0x56
Address 0x103: 0x12 Address 0x103: 0x78
The order of bytes will be reversed in eight-byte data between the little endian and the big endian.
Little Endian: Address 0x100: 0xef Big Endian: Address 0x100: 0x01
Address 0x101: 0xcd Address 0x101: 0x23
Address 0x102: 0xab Address 0x102: 0x45
Address 0x103: 0x89 Address 0x103: 0x67
Address 0x104: 0x67 Address 0x104: 0x89
Address 0x105: 0x45 Address 0x105: 0xab
Address 0x106: 0x23 Address 0x106: 0xcd
Address 0x107: 0x01 Address 0x107: 0xef
Members of compound-type and class-type data will be allocated in the same way as that of the little endian. However, the order of byte data of each member will be reversed according to the rule of data size.
Little Endian: Address 0x100: 0x34 Big Endian: Address 0x100: 0x12
Address 0x101: 0x12 Address 0x101: 0x34
Address 0x102: Unused area Address 0x102: Unused area
Address 0x103: Unused area Address 0x103: Unused area
Address 0x104: 0xbc Address 0x104: 0x56
Address 0x105: 0x9a Address 0x105: 0x78
Address 0x106: 0x78 Address 0x106: 0x9a
Address 0x107: 0x56 Address 0x107: 0xbc
Bit fields will be allocated in the same way as that of the little endian. However, the order of byte data in each area will be reversed according to the rule of data size.
Little Endian: Address 0x100: 0x01 Big Endian: Address 0x100: 0x00
Address 0x101: 0x00 Address 0x101: 0x01
Address 0x102: 0x01 Address 0x102: 0x00
Address 0x103: 0x00 Address 0x103: 0x01
Address 0x104: 0x01 Address 0x104: 0x00
Address 0x105: 0x00 Address 0x105: 0x01
Address 0x106: Unused area Address 0x106: Unused area
Address 0x107: Unused area Address 0x107: Unused area
Floating-point numbers handled by this compiler are internally represented in the standard IEEE format. This section outlines the internal representation of floating-point numbers in the IEEE format.
This section assumes that the dbl_size=8 option is specified. When the dbl_size=4 option is specified, the internal representation of the double type and long double type is the same as that of the float type.
float types are represented in the IEEE single-precision (32-bit) format, while double types and long double types are represented in the IEEE double-precision (64-bit) format.
Figure 4.1 shows the structure of the internal representation of float, double, and long double types.
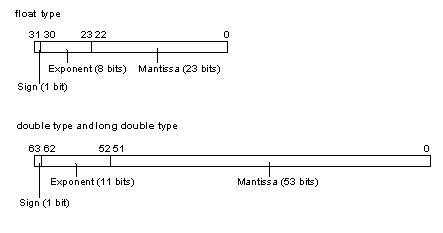
The internal representation format consists of the following parts:
Shows the sign of the floating-point number. 0 is positive, and 1 is negative.
Shows the exponent of the floating-point number as a power of 2.
Shows the data corresponding to the significant digits (fraction) of the floating-point number.
In addition to the normal real numbers, floating-point numbers can also represent values such as infinity. The following describes the types of values represented by floating-point numbers.
Represents a normal real value; the exponent is not 0 or not all bits are 1.
Represents a real value having a small absolute number; the exponent is 0 and the mantissa is other than 0.
Represents the value 0.0; the exponent and mantissa are 0.
Represents infinity; all bits of the exponent are 1 and the mantissa is 0.
Represents the result of operation such as "0.0/0.0", "∞/∞", or "∞–∞", which does not correspond to a number or infinity; all bits of the exponents are 1 and the mantissa is other than 0.
Table 4.4 shows the types of values represented as floating-point numbers.
Denormalized numbers are floating-point numbers of small absolute values that are outside the range represented by normalized numbers. There are fewer valid digits in a denormalized number than in a normalized number. Therefore, if the result or intermediate result of a calculation is a denormalized number, the number of valid digits in the result cannot be guaranteed. |
The float type is internally represented by a 1-bit sign, an 8-bit exponent, and a 23-bit mantissa.
The sign indicates the sign of the value, either 0 (positive) or 1 (negative). The exponent is between 1 and 254 (28 – 2). The actual exponent is gained by subtracting 127 from this value. The range is between –126 and 127. The mantissa is between 0 and 223 – 1. The actual mantissa is interpreted as the value of which 223rd bit is 1 and this bit is followed by the decimal point. Values of normalized numbers are as follows:
(–1)sign × 2exponent–127 × (1 + (mantissa) × 2–23)
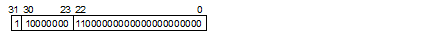
Exponent: 10000000(2) – 127 = 1, where (2) indicates binary
The sign indicates the sign of the value, either 0 (positive) or 1 (negative). The exponent is 0 and the actual exponent is –126. The mantissa is between 1 and 223–1, and the actual mantissa is interpreted as the value of which 223rd bit is 0 and this bit is followed by the decimal point. Values of denormalized numbers are as follows:
(–1)sign × 2–126 × ((mantissa) × 2–23)
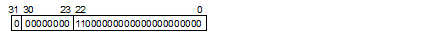
Mantissa: 0.11(2) = 0.75, where (2) indicates binary
The sign is 0 (positive) or 1 (negative), indicating +0.0 or –0.0, respectively. The exponent and mantissa are both 0.
+0.0 and –0.0 are both the value 0.0.
The sign is 0 (positive) or 1 (negative), indicating +∞ or –∞, respectively.
The mantissa is a value other than 0.
A not-a-number is called a quiet NaN when the MSB of the mantissa is 1, or a signaling NaN when the MSB of the mantissa is 0. There are no stipulations regarding the values of the rest of the mantissa and of the sign. |
The double and long double types are internally represented by a 1-bit sign, an 11-bit exponent, and a 52-bit mantissa.
The sign indicates the sign of the value, either 0 (positive) or 1 (negative). The exponent is between 1 and 2046 (211–2). The actual exponent is gained by subtracting 1023 from this value. The range is between –1022 and 1023. The mantissa is between 0 and 252–1. The actual mantissa is interpreted as the value of which 252nd bit is 1 and this bit is followed by the decimal point. Values of normalized numbers are as follows:
(–1)sign × 2exponent–1023 × (1+(mantissa) × 2–52)
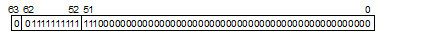
Exponent: 1111111111(2) –1023 = 0, where (2) indicates binary
The sign indicates the sign of the value, either 0 (positive) or 1 (negative). The exponent is 0 and the actual exponent is –1022. The mantissa is between 1 and 252–1, and the actual mantissa is interpreted as the value of which 252nd bit is 0 and this bit is followed by the decimal point. Values of denormalized numbers are as follows:
(–1)sign × 2–1022 × ((mantissa) × 2–52)
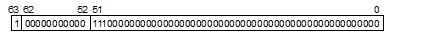
Mantissa: 0.111(2) = 0.875, where (2) indicates binary
The sign is 0 (positive) or 1 (negative), indicating +0.0 or –0.0, respectively. The exponent and mantissa are both 0.
+0.0 and –0.0 are both the value 0.0.
The sign is 0 (positive) or 1 (negative), indicating +∞ or –∞, respectively. The exponent is 2047 (211–1).