|
関数の計算結果がdouble型の値として表せない時、あるいはオーバフロー/アンダフローとなった時、errnoに設定する値です。 |
||
|
2番目の引数型がlong double,引数同士が等しい場合に、2番目の引数をその関数の型に変換して返す以外は、nextafter関数群と同じです。 |
||
関数に入力するパラメータの値が関数内で定義している値の範囲を超えている時、定義域エラーが発生します。この時errnoにはEDOMの値が設定されます。また、関数のリターン値は、処理系定義です。
関数における計算結果がdouble型の値として表せない時には範囲エラーが発生します。この時、errnoにはERANGEの値が設定されます。また、計算結果がオーバフローの時は、正しく計算が行われた時と同様の符号のHUGE_VAL、 HUGE_VALFあるいは HUGE_VALLの値をリターン値として返します。逆に計算結果がアンダフローの時は、0をリターン値として返します。
.
.
.
1 x=asin(a);
2 if (errno==EDOM)
3 printf("error\n");
4 else
5 printf("result is : %lf\n",x);
.
.
.
1行目で、asin関数を使って逆正弦値を求めます。このとき、実引数aの値が、asin関数の定義域[-1.0, 1.0]の範囲を超えていると、errnoに値EDOMが設定されます。2行目で定義域エラーが生じたかどうかの判定をします。定義域エラーが生じれば、3行目で、errorを出力します。定義域エラーが生じなければ5行目で、逆正弦値を出力します。
範囲エラーが発生するかどうかは、コンパイラによって定まる、浮動小数点型の内部表現形式によって異なります。例えば無限大を値として表現できる内部表現形式を採用している場合、範囲エラーの生じないように<math.h>のライブラリ関数を実現することができます。 |
|
非数を返します。非数の形式は「4.1.5 データの内部表現と領域」の「(5) 浮動小数点型の仕様」を参照してください。 |
||
|
errnoにERANGEを設定する関数については、「10.5.6 C標準ライブラリ関数のエラーメッセージ」を参照してください。上記以外は設定しません。 |
||
|
fmodの戻り値の詳細は、「7.4.7 <math.h>」の「fmod / fmodf / fmodl」を参照してください。 |
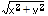 )を計算します。
)を計算します。